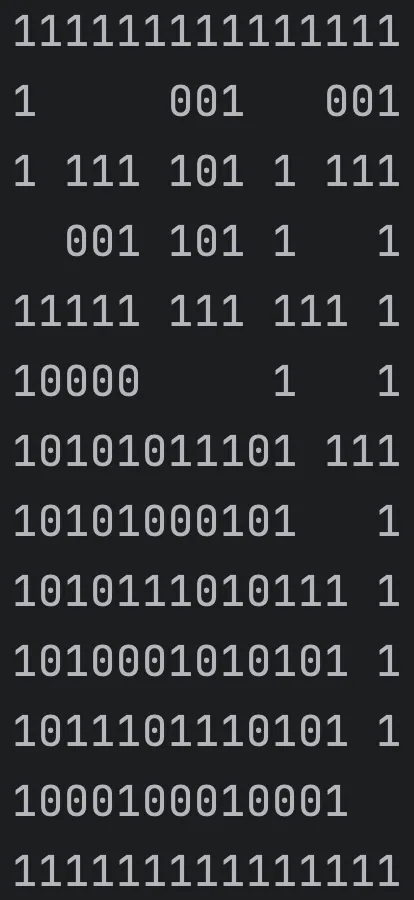
For this project, I developed a program that reads a representation of a maze and solves it. The goal of this project is to demonstrate that graphs can be used to model gain insight into problems and chart a suitable solution for them. Graphs are built based on a relationship between entities. In the case of a graph, entities are squares that form the maze and the relationship is "is-adjacent-to".
Learning Objectives
- - C++ written solution
- - Applications of the stack data structure
- - Backtracking algorithms work in solving search problems
- - Use of graphs in a setting that is simple and familiar
The input maze is surrounded by ones (walls) except for the start and the target cells, which are zeros. They can be anywhere on the boundary of the maze. Two open cells are adjacent if one is on the left, right, above, and below the other. You can move from one cell to one of its adjacent cells if both cells represent path cells. The objective is to find a path from one side of the boundy to the next.
Input:

How my program works...
I used a backtracking algorithm to find a path between the start and the target cells. The process begins at the start cell and moves from one cell to the next, by applying a particular rule, until either I end up at the target cell, in which case the algorithm stops, or I reach a dead end, in which case we backtrack. That is, we take one or more steps backward until we get to a point where we can move in a different direction.
The output of your program is exactly like its input, except you would print a blank character in place zeros of the cells on the path. As seen below.
Output: